Produkter Kategori
- FM Transmitter
- 0-50w 50w-1000w 2kw-10kw 10kw +
- TV Transmitter
- 0-50w 50-1kw 2kw-10kw
- FM-antenne
- TV-antenne
- Antenne tilbehør
- Kabeler Stik Power Splitter Dummy Load
- RF Transistor
- Strømforsyning
- Audio Udstyr
- DTV frontend Udstyr
- Link System
- STL-system Microwave Link system
- FM-radio
- Power Meter
- Andre produkter
- Specielt til Coronavirus
Produkter Tags
Fmuser steder
- es.fmuser.net
- it.fmuser.net
- fr.fmuser.net
- de.fmuser.net
- af.fmuser.net -> Afrikaans
- sq.fmuser.net -> albansk
- ar.fmuser.net -> arabisk
- hy.fmuser.net -> Armensk
- az.fmuser.net -> aserbajdsjansk
- eu.fmuser.net -> baskisk
- be.fmuser.net -> hviderussisk
- bg.fmuser.net -> Bulgarian
- ca.fmuser.net -> Catalansk
- zh-CN.fmuser.net -> Kinesisk (forenklet)
- zh-TW.fmuser.net -> Kinesisk (traditionelt)
- hr.fmuser.net -> Kroatisk
- cs.fmuser.net -> Tjekkisk
- da.fmuser.net -> dansk
- nl.fmuser.net -> Hollandsk
- et.fmuser.net -> estisk
- tl.fmuser.net -> filippinsk
- fi.fmuser.net -> finsk
- fr.fmuser.net -> Fransk
- gl.fmuser.net -> galicisk
- ka.fmuser.net -> Georgisk
- de.fmuser.net -> tysk
- el.fmuser.net -> Greek
- ht.fmuser.net -> haitisk kreolsk
- iw.fmuser.net -> hebraisk
- hi.fmuser.net -> hindi
- hu.fmuser.net -> Hungarian
- is.fmuser.net -> islandsk
- id.fmuser.net -> Indonesisk
- ga.fmuser.net -> Irsk
- it.fmuser.net -> Italiensk
- ja.fmuser.net -> japansk
- ko.fmuser.net -> koreansk
- lv.fmuser.net -> lettisk
- lt.fmuser.net -> Litauisk
- mk.fmuser.net -> Makedonsk
- ms.fmuser.net -> malaysisk
- mt.fmuser.net -> maltesisk
- no.fmuser.net -> Norwegian
- fa.fmuser.net -> persisk
- pl.fmuser.net -> polsk
- pt.fmuser.net -> portugisisk
- ro.fmuser.net -> Romanian
- ru.fmuser.net -> russisk
- sr.fmuser.net -> serbisk
- sk.fmuser.net -> Slovakisk
- sl.fmuser.net -> Slovensk
- es.fmuser.net -> spansk
- sw.fmuser.net -> swahili
- sv.fmuser.net -> svensk
- th.fmuser.net -> Thai
- tr.fmuser.net -> tyrkisk
- uk.fmuser.net -> ukrainsk
- ur.fmuser.net -> Urdu
- vi.fmuser.net -> Vietnamesisk
- cy.fmuser.net -> walisisk
- yi.fmuser.net -> Jiddisch
Decibel-tutorial: dB og dBm vs. Gain and Milliwatts
Begrebet decibel (dB) er forståeligt vanskeligt og forvirrende for nogen, der netop bliver introduceret til det. Kombination af specifikationer for forstærkning, effekt og spænding (og strøm, men ikke så ofte), der blander dB, dBm, dBW, watt, milliwatt, spænding, millivolt osv. Kræver ofte konvertering frem og tilbage mellem lineære værdier og decibelværdier. Denne korte tutorial hjælper med at klarlægge forskellen mellem at arbejde med decibel og arbejde med lineære værdier.
Logaritmer (logfiler) blev først udtænkt i de tidlige 1600s af den skotske matematiker John Napier, som et værktøj til at forenkle multiplikations- og divisionsoperationer ved at konvertere dem til henholdsvis hurtigere og mindre fejlutsatte additions- og subtraktionsoperationer. Dette gøres muligt på grund af den måde, man kan opnå multiplikation af to tal udtrykt som lignende basisnumre med eksponenter ved blot at tilføje eksponenterne sammen. Opdelingen af de samme numre opnås ved at trække eksponenterne fra. Det er en af eksponenternes love og ser sådan ud:
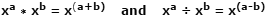
Brug af faktiske tal som et eksempel, hvor x = 10, a = 4, b = 1:
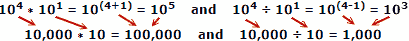
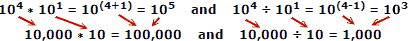
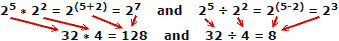
Folk har en tendens til at begå færre fejl, når de tilføjer og fratrækker tal, så fordelen med logaritmer er åbenbar. Husk, at logaritmer blev udviklet, før automatiske mekaniske eller elektroniske computere var tilgængelige. En diasregel udnytter logaritmernes egenskaber til beregning, men det er et separat hovedemne.
Dette er enkle eksempler, men gælder for enhver base eller eksponent. I mangel af en lommeregner har du brug for en tabel med numre og deres tilsvarende logaritmer for at være nyttige til generel anvendelse. Tidlige logtabeller udfyldte bind, afhængigt af afstanden mellem tal (1.000, 1.001, 1.002, 1.003, vs. 1.0, 1.1, 1.2, 1.3 osv.). Den gode nyhed for skabere af logaritmetabeller er, at kun et enkelt 'årti' med tal (f.eks. 1 til 10) er påkrævet, da hvert foregående eller afslutende årti er en simpel multipel af en magt af 10.
Bemærk: Jeg bruger base 10 i denne diskussion, da det er basen i vores fælles talesystem - derav udtrykket 'fælles logaritme' for base 10-logfiler. Du har måske hørt om naturlige logaritmer, der bruger basen til e, men e bruges ikke meget ofte, når man beregner skalær elektrisk strøm, spænding og strømmængder (selvom det bruges, når fasevinkler er inkluderet, dvs. Eulers identitet). Naturlige logaritmer skrives som ln (x) uden 'e' -underskriptet, hvorimod base 10-logaritmer normalt skrives blot som log (x) uden 10-underskriften; dvs. ikke henholdsvis loge (x) eller log10 (x).
Pr. Base = 10 log-tabel:
Semi-logaritmisk 5 Cycles Engineering Grafisk papir - RF Cafe Undtagelsen og specialtilfælde er logx (0) = Ikke defineret. Det er sådan, fordi der ikke er nogen magt, som du kan hæve et hvilket som helst tal og få 0 (nul). Du kan asymptotisk nærme dig nul, men du kan ikke komme til nul. Der vises aldrig tallet nul i en logskala; de løber normalt fra en eller anden kraft af 10 til en anden magt på ti. Et eksempel på loggrafipapir vises til højre. Det har 5 'cykler' eller 'årtier' af rækkevidde. Bemærk, at der ikke er nogen nul på y-aksen.
Basen-10 (almindelig) logaritme for et tal er den eksponent, som 10 skal hæves til for at få dette nummer. Med andre ord, da 10 hævet til effekten af 2 er lig med 100 (102 = 100), er basen-10-loggen til 100 2 (log10 100 = 2).
Dette er den grundlæggende lov for logaritmer:
Udførelse af de samme multiplikationer og opdelinger som gjort øverst på siden ved hjælp af faktiske logaritmer:
Det er fint, men hvad du ender med er logaritmen for det nummer, du søger. Spørgsmål: Bortset fra et simpelt eksempel som dette, hvordan får du det svar, du har brug for? Svar: Slå op til antilogaritmen (antilog) af resultatet. I dette tilfælde:
HP-35-regnemaskine (wikipedia) - RF CafeSiden logaritmen til 'x' er lig med 1.8444, den antilog er lig med 'x', som er 69.9
Jeg brugte min lommeregner til at slå logfiler og antilogs til disse numre, men inden 1972, da Hewlett Packard (HP) introducerede deres HP-35 videnskabelige regnemaskine, var den gennemsnitlige person uden adgang til en virksomheds- eller universitets mainframe-computer brug for en log tabel for at udføre sådanne beregninger.
Hvem generer at bruge logaritmer i dag, spørger du måske? Masser af mennesker, inklusive mig, ofte når man beregner kaskaderede systemparametre som støjtal (NF) og aflytningspunkter (IP). Enkel tilføjelse og subtraktion af forøgelse dB og effekt dBm værdier fungerer ikke med NF og IP. De styrende formler bruger multiplikation og opdeling af lineær forstærkning og effektværdier, som kræver først at konvertere dB og / eller dBm til lineære tal (forstærkningsforhold og mW) ved hjælp af antilogs, udføre kaskadeberegningerne og derefter konvertere resultatet tilbage til dB og / eller dBm ved hjælp af logfiler.
Ikke alle systemkaskadefunktioner kræver konvertering frem og tilbage. Hvis det kun er nødvendigt med den samlede systemforstærkning og / eller udgangseffektniveau, kan beregninger udføres med enten lineære enheder (mW og multiplikatorer) eller logaritmiske enheder (henholdsvis dBm og dB).
Definitionen af 'dB' og 'dBm'
En decibel (dB) i elektroteknik er defineret som 10 gange base-10-logaritmen med et forhold mellem to effektniveauer; f.eks Pout / Pin (gain, med andre ord). For at vide:
Alle gevinster større end 1 udtrykkes derfor som positive decibel (> 0), og gevinster på mindre end 1 udtrykkes som negative decibel (<0). Bemærk, at i de tilfælde, de fleste af os støder på, skal det lineære forhold mellem P1 / P2 være et positivt tal (> 0), da logaritmen på 0 er udefineret, og logaritmen til negativtal er kompleks (de indeholder både en reel og en imaginær del ). DB-værdien kan dog teoretisk få en hvilken som helst værdi mellem −∞ og + ∞ inklusive 0, hvilket er en forstærkning på 1 [10 * log (1) = 0 dB].
'dBm' er en decibel-baseret enhed, der henvises til 1 mW. Da 0 dB forstærkning er lig med en forstærkning på 1, er 1 mW effekt 0 dB større end 1 mW eller 0 dBm. Tilsvarende er en effektenhed på dBW decibel i forhold til 1 W effekt.
I overensstemmelse hermed er alle dBm-værdier større end 0 større end 1 mW, og alle dBm-værdier mindre end 0 er mindre end 1 mW (se fig. 1). For eksempel er + 3.01 dBm 3.01 dB større end 1 mW; dvs. eller 0 dBm + 3.01 dB = + 3.01 dBm (2 mW). −3.01 dBm er 3.01 dB mindre end 1 mW; dvs. eller 0 dBm + (−3.01) dB = −3.01 dBm (0.5 mW).
Følgende tabel giver nogle numeriske eksempler, så du kan se sammenhængen mellem mW og dBm. Det samme sæt værdier, der er afbildet i en logaritmisk skala, ville frembringe en lige linje. På grund af det logaritmiske forhold bundter grafen de mindre værdier mod den venstre lodrette akse. En forstørret version af området 0 til 1 mW er indsat for klarhed.
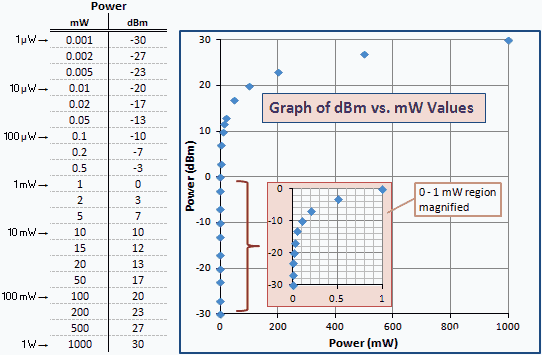
Fig. 1 - Graf over strøm i enheder af dBm vs. mW
Fig. 2 er en tabel og en graf over dB vs. lineære forstærkningsforhold svarende til dBm vs. mW i fig. 1. Bemærk, at numrene og kurverne er nøjagtigt de samme; kun akseetiketterne ændres. Dette skyldes, at dBm er en magtenhed udtrykt i dB i forhold til 1 mW (0 dBm).
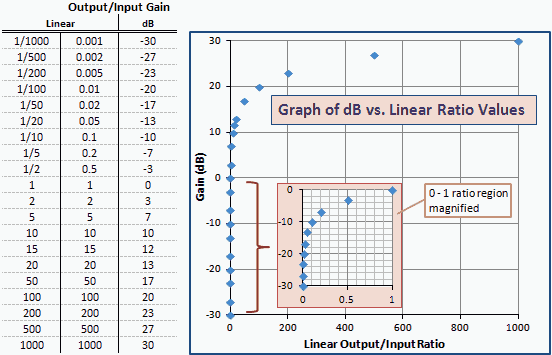
Fig. 2 - Graf over gevinst i enheder med dBm vs. lineær ratio
0 dBm + 6.02 dB = 6.02 dBm
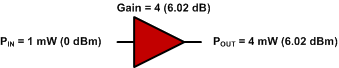
Fig. 3 - Forstærkning af en enkelt forstærker.
Hvis et 1 mW-signal (0 dBm) føres ind i forstærkeren, kommer 4 mW ud af den første forstærker, og 24 mW kommer ud af den anden forstærker. Se fig. 4.
1 mW * 4 * 6 = 24 mW
0 dBm + 6.02 dB + 7.78 dB = 13.8 dBm

Fig. 4 - Kaskadeforstærket dobbeltforstærker.
Kombination af gevinst og tab (lineær og dB)
Dette næste eksempel viser, hvad der sker, når der opstår en forstærkning <1 (et tab), hvor en dæmper med en forstærkning på 1/6 placeres efter den første forstærker i stedet for at have en anden forstærker. Se fig. 5.
4 * 1 / 6 = 2 / 3 (lineær forstærkning). Tilsvarende 6.02 dB - 7.78 dB = −1.76 dB (decibelforstærkning).
Som med det foregående eksempel, hvis et 1 mW-signal (0 dBm) føres ind i forstærkeren med en forstærkning på 4, kommer 4 mW ud. Denne 4 mW går derefter ind i dæmperen med en lineær forstærkning på 1 / 6 og kommer ud på et effektniveau på 4 / 6 mW (2 / 3 mW).
Den samlede forstærkning i dette tilfælde er 4 / 6 = 2 / 3, så udgangseffekten vil faktisk være mindre end indgangseffekten.
1 mW * 4 * 1 / 6 = 2 / 3 mW = 0.67 mW
0 dBm + 6.02 dB + (-7.78 dB) = −1.76 dBm

Fig. 5 - Forstærket forstærker og dæmpningsanordning.
12 mW + 34 mW + 8 mW + 20 dB
Supplerende oplysninger om logaritmer
Logaritmer af produkter
En egenskab med logaritmer, der anvendes implicit ovenfor, angiver følgende og er grundlaget for at være i stand til at tilføje og trække logaritmeværdier i stedet for at multiplicere deres lineære ækvivalenter.
'h * j / k * m / n' kan repræsentere en kaskade af komponenter, der har tre enheder (h, j og m) hver med forstærkning> 1 og to enheder (k og n) hver med forstærkning <1 (se Fig. 6). Den samlede systemforstærkning kan beregnes ved enten at multiplicere alle de lineære forstærkningsværdier sammen eller tilføje alle decibelforstærkningsværdierne sammen.

Fig. 6 - Kaskaderede komponenter
Det følgende er vigtigt for at forstå, hvorfor effektforøgelse med hensyn til effekt er 10 * log (Pout / Pin) dB, mens strømforstærkning med hensyn til spænding er 20 * log (Vout / Vin) dB.
hvilket er så fordi cf er lig med c ganget med sig selv 'f' gange. For eksempel, hvis f = 4:
Power Gain Baseret på Power vs. Power Gain Baseret på spænding
Effektforstærkning er åbning / pin, og spændingsforstærkning er Vout / Vin. Effektforstærkning baseret på et effektforhold i decibel er defineret som 10 * log (træk / pin). Effektforøgelse med hensyn til spænding er [(Vout2 / R) / (Vin2 / R)], da per Ohms lov P = V2 / R. 'R' i nævnerne annullerer forlader Vout2 / Vin2, hvilket er lig med (Vout / Vin) 2, som defineret ved reglen for eksponenter, der siger ac / bc = (a / b) c. Derfor:
Vigtigt: Spændingsforstærkning med hensyn til spænding er 10 * log (Vout / Vin) dB, det samme som med effektforstærkning med hensyn til effekt. Det er kun, når strømforstærkning udtrykkes som spænding, at 20 * log (Vout / Vin) dB-ligningen gælder. Dette er et fælles forvirringspunkt.
Ingen operation i matematik er vilkårlig, og det er grunden til, at et signaleffekttab (forstærkning <1) bliver portrætteret som en negativ værdi og derfor trækkes under en kaskadeberegning. Det er en simpel demonstration, men værd at nævne.
log (1 / f) = log (1) - log (f) = 0 - log (f) = -log (f)
Hvis du gerne vil bygge en radiostation, skal du booste din FM-radiosender eller have brug for andre FM-udstyr, er du velkommen til at kontakte os: [e-mail beskyttet].

