Kraft og amplitude: watt, volt og refererede decibel

Introduktion
I radiofrekvensapplikationer (men også i en masse anden applikation) er det meget almindeligt at håndtere meget store og meget små signaler. For eksempel kan en transceiver muligvis sende en effekt på 100 W og kun modtage 10 fW (eller 0.000'000'000'000'01 W). Disse ekstremt forskellige effektniveauer kan have de samme kredsløb. Naturligvis kan disse tal udtrykkes i Watts ved hjælp af den tekniske notation (som ovenfor) eller med den videnskabelige notation, ligesom 1 · 102 W og 1 · 10 – 14 W, men de er ret vanskelige at udtale, og hvis eksponenten er forkert stavet , vil den resulterende fejl være enorm.

En anden måde er at tage logaritmen og konvertere alle kræfterne i dBm. 100 W bliver + 50 dBm og 10 fW bliver –110 dBm: disse tal er meget lettere at håndtere uden besvær og at skrive. Hvis dæmpning og forstærkning af forskellige kredsløbsblokke også udtrykkes i dB, for at finde den endelige effekt, kan man blot tilføje alt sammen i stedet for at multiplicere, hvilket yderligere forenkler beregningerne.

Ikke alle har det godt med dB, dBm og lignende (pseudo) enheder: der er ikke noget strengt behov for at bruge dem, men de er så vidt brugt inden for teknik, at det er meget vanskeligt at undgå dem.

Nogle teori
Decibel (dB) bruges til at udtrykke magtforhold på en logaritmisk måde, så meget store og meget små kræfter kan sammenlignes ved hjælp af komfortable tal. En decibel er en dimensionløs pseudo-enhed, fordi den er defineret af forholdet mellem to kræfter. Men da decibel er så praktisk at udtrykke ægte magt i stedet for kun et dimensionsløst forhold, bruges refererede decibel meget ofte.

Hvis vi taler om magt, definerer følgende ligning effektniveauet P i dB af effekten p i W henvist til effekten p0:

10-faktoren skyldes, at decibel er "tiende af klokkerne". Men jeg har aldrig hørt om nogen måling udført i Bells, kun decibel bruges.

Den mest almindelige enhed er dBm (udtales "dBm") også kendt som dBmW eller decibel-milliwatt: det er bare effektniveauet i dB sammenlignet med en referenceeffekt på p0 = 1 mW. Nogle gange bruges også dBW, og de udtrykker effektforholdet i forhold til p0 = 1 W, men de er ikke meget almindelige.

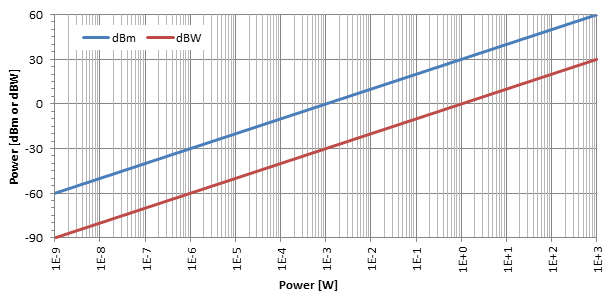
Som vist i ovenstående plot er den logaritmiske virkning af decibelomdannelsen ganske tydelig. Som man kan se på dette log-lin plot er dBm og dBW blot to lige linjer adskilt af 30 dB: for at konvertere dBm til dBW skal du blot trække 30.

I nogle domæner, som analog tv-modtagelse, er det almindeligt at måle spænding i stedet for strøm. Dette er ikke et problem, så længe impedansen er kendt og rettet (tv-modtagere bruger normalt 75 Ω).

Absolute spændinger kan også drage fordel af den decibel logaritmiske skala ved at bruge decibel-mikrovolt (dBμV) og desibel-volt (dBV). Den mest almindelige er dBμV, der udtrykker spændingsforholdet i forhold til u0 = 1 μV. Nogle gange bruges dBV også, og de udtrykker spændingsforholdet i forhold til u0 = 1 V.

Pas på, at spændinger bruger en "20" i stedet for en "10" i deres dB-formel. Dette skyldes, at decibel altid defineres som kraftrationer; hvis vi kun har spændinger, skal vi først kvadratere dem for at finde kraften. Denne magt af to, når den tages ud af logaritmen, multiplicerer den eksisterende faktor 10 med 2.

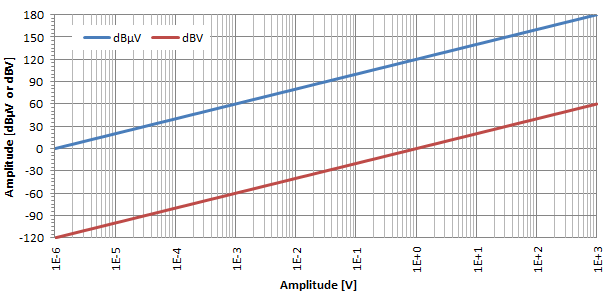
Som vist i ovenstående plot og på en lignende måde som før, er den logaritmiske virkning af decibelomdannelsen ganske tydelig også for spændinger. Som man kan se på dette log-lin plot er dBμV og dBV blot to lige linjer adskilt af 120 dB: for at konvertere dBμV til dBV skal du blot trække 120.

Hvis vi nu vil konvertere fra strøm til spænding og omvendt, er vi nødt til at kende impedansen. Vi bruger bare følgende ligning:

Denne konvertering er kun gyldig, når impedansen Zc er reel, og belastningen matches med transmissionslinjen.

Hvis vi plotter effektniveauet i dBm og amplitudeniveauet i dBμV som en funktion af effekten i W for en given impedans (her Zc = 50 Ω) får vi følgende:

Som før har vi to parallelle linjer 107 dB fra hinanden. Så for at konvertere fra dBm til dBμV skal du blot tilføje 107 dB for Zc = 50 Ω, tilføje 109 dB for Zc = 75 Ω, tilføje 115 dB for Zc = 300 Ω eller tilføje 118 dB for Zc = 600 Ω.

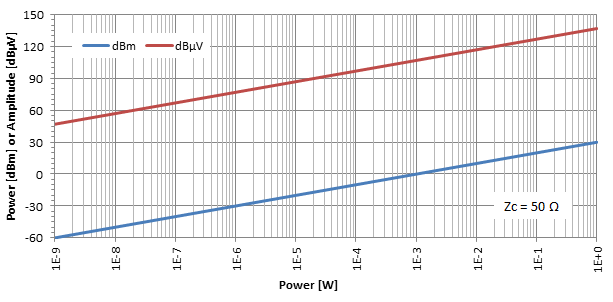
Praktiske overvejelser
Ved første øjekast kan man tro, at en lommeregner på grund af logaritmen er absolut nødvendig for at håndtere dBm. Faktisk kan en grov beregning let gøres i dit hoved. Du skal bare huske tre fakta:
 En effekt på 1 mW er 0 dBm.
 Hver gang strømmen fordobles, tilføj 3 dB.
 Hver gang strømmen øges med en faktor 10, tilføj 10 dB.

Lad os nu overveje et par eksempler: Antag, at vi har et effektniveau på 26 dBm. Vi kan skrive 26 dBm = 0 dBm + 10 dB + 10 dB + 3 dB + 3 dB, og med de foregående tre enkle regler kan vi nemt finde kraften ved at gøre 1 mW · 10 · 10 · 2 · 2 = 400 mW .

Et andet eksempel: Antag, at vi har –33dBm: vi kan skrive som –33 dBm = 0 dBm - 10 dB - 10 dB - 10dB - 3 dB, og vi finder 1 mW / 10 / 10 / 10 / 2 = XUM

Dette fungerer også på anden måde, f.eks. Er 50 mW bare 1 mW · 10 · 10 / 2. I dBm har vi 0 dBm + 10 dB + 10 dB –3 dB = 17 dBm.

Dette kræver lidt øvelse, men er meget let at gøre. Det er ikke så nøjagtigt som en lommeregner, fordi du kun kan være nøjagtig ved ± 2 dB, men for indsatsen giver du en meget god idé om styrken af ​​et signal.

En lignende metode fungerer også for dBμV, men reglerne er forskellige:
 En amplitude på 1 μV er 0 dBμV.
 Hver gang amplituden fordobles, tilføj 6 dB.
 Hver gang amplituden øges med en faktor 10, tilføj 20 dB.

Du kan blive overrasket over beregningerne i decibel vist før, hvor dB føjes til dBm, hvilket er ganske mærkeligt. Dette skyldes, at decibel er pseudo-enheder og ikke opfører sig som sædvanligt. Forholdet mellem to kræfter er udtrykt i dB, men er uden dimensioner: for eksempel betyder 3 dB kun "dobbelt så meget". Kraften udtrykt i dBm er virkelig en effekt: for eksempel betyder 10 dBm "10 gange stærkere end 1 mW", hvilket er 10 mW.

Når du tilføjer decibel (dB, dBm, ...) på grund af deres logaritmiske karakter, multiplicerer du faktisk de oprindelige figurer sammen. Så hvis du tilføjer en gevinst på 3 dB til en magt på 10 dBm, får du 13 dBm. Men hvad du virkelig gjorde, er at multiplicere en faktor af 2 med en effekt på 10 mW og få 20 mW, hvilket er 13 dBm!

Indtil videre så godt, at tilføje er meget lettere at gøre i dit hoved end at multiplicere, og dette gør decibel så praktisk. Men der er et problem: da tilføjelse af decibel sammen svarer til at multiplicere de originale faktorer, hvordan kan man tilføje (kombinere) kraften i to signaler? Det kan du ikke. Du kan ikke tilføje dBm til dBm. Hvis du for eksempel har et kredsløb eller en enhed, der kombinerer effekten af ​​et signal på 10 dBm (10 mW) med kraften fra et andet signal på 13 dBm (20 mW), er resultatet 10 mW + 20 mW = 30 mW, hvilket er 14.8 dBm. Der er ingen måde at gøre dette direkte i dBm, du er nødt til at konvertere begge kræfter i Watts, tilføje dem sammen og konvertere dem tilbage i dBm. Dette er en stor begrænsning af decibel og en fælles faldgrube; heldigvis er denne operation ikke særlig almindelig.

Hvis du gerne vil bygge en radiostation, skal du booste din FM-radiosender eller have brug for andre FM-udstyr, er du velkommen til at kontakte os: [e-mail beskyttet].

Læg en besked 

Message List